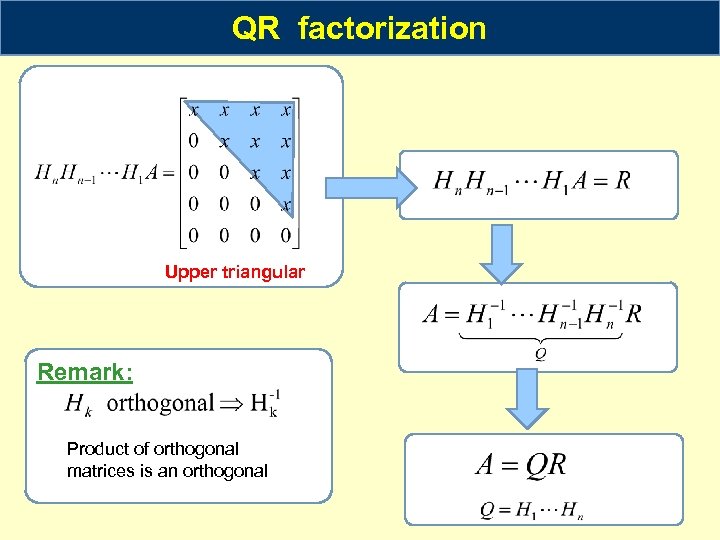
Qr Householder Method

subsflecmoggaquepor.netlify.com › ★ Qr Householder Method

This paper) that the Gaussian-elimination and Householder methods for upper-triangularization are on the order of n3. Thus, these methods are far more eﬃcient than naive cofactor expansion. 1.3 Computation of matrix inverses In elementary linear algebra, we are taught to compute inverses using cofactor expansion. Householder reﬂector LVF pp.161. Like LU decomposition, Householder transformation zeros out elements A(i + 1: n,i) column by column. X x x x x x x x x x x x ⇒ x x x 0 x x 0 x x 0 x x ⇒ x x x 0 x x 0 0 x 0 0 x ⇒ x x x 0 x x 0 0 x 0 0 0. QR decomposition You are encouraged to solve this task according to the task description. The method of Householder reflections should be used: Method. Multiplying a given vector, for example the first column of matrix, with the Householder matrix, which is given as =. Lecture 3: QR-Factorization This lecture introduces the Gram–Schmidt orthonormalization process and the associated QR-factorization of matrices. It also outlines some applications of this factorization. This corresponds to section 2.6 of the textbook. In addition, supplementary information on other algorithms used to produce QR-factorizations. Then the QR factorization is unique. Our aim is to compute (2.1) by the numerically more stable method of Householder reflections, which has apparently not been done before. The very first step introduces the crucial question: What could it mean to map a function onto another function that is ‘zero below the diagonal’?

$initialize$So far, we have only shown existence , but How do we compute QR decompositions?

Householder Reflections

Householder reflection is $H=I-2vv'$ where $norm v2=1$ which reflects over hyperplane orthogonal to $v$

Lemma. Householder reflections are orthogonal matrices

Proof. $~$ HOMEWORK

We use a series of Householder reflections to reduce $APi$ to an upper triangular matrix, and the resultant product of Householder matrices gives us $Q,$, i.e. $$underbrace{H_rcdots H_1}_{Q'}APi=R$$

First, find $H_1$ that makes every entry below $R_{11}$ zero,
begin{align*}
H_1a_1&=R_{11}e_1
R_{11}e_1&=a_1-2v_1v_1'a_1
v_1(underbrace{2v_1'a_1}_text{scalar})&=a_1-R_{11}e_1
implies~v_1&=frac{a_1-R_{11}e_1}{norm{a_1-R_{11}e_1}2}
implies~R_{11}e_1&=pmnorm{a_1}2
v_1&=frac{a_1-norm{a_1}{}e_1}{norm{vphantom{big };!a_1-norm{a_1}{}e_1}2}
implies H_1&=I-frac{(a_1-norm{a_1}{}e_1)(a_1-norm{a_1}{}e_1)'}{norm{vphantom{big };!a_1-norm{a_1}{}e_1}{}_2^2}
end{align*}

Then, we have
$$H_aAPi~=~defhmatres{{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!mat{&&&tilde{A}_2&&&}end{matrix}end{matrix}}}left[{begin{matrix}begin{matrix}R_{11}&text{--------------}~~end{matrix}begin{matrix}begin{matrix}0vdots0&end{matrix}&!!!!!!underbrace{mat{&&&tilde{A}_2&&&}}_text{repeat on these}end{matrix}end{matrix}}^{vphantom{Big }}right]$$

Givens Rotations

Givens rotations $Gij$ where $Gij$ is the identity matrix except
- $Gij_{ii}=Gij_{jj}=lambda$
- $Gij_{ij}=sigma$
- $Gij_{ji}=-sigma$

$$text{for example, },G^{(2,4)}=mat{1&0&0&00&lambda&0&sigma0&0&1&00&-sigma&0&lambda}$$

HOMEWORK $~$ Show that Givens rotation is orthogonal when $sigma^2+lambda^2=1$

We can also use Givens rotations to compute the decomposition, so that $$underbrace{G_Tcdots G_1}_{Q'}APi=R$$

To find $G_1$, we look for a Givens rotation $G^{(1,2)}$ that will make the entry in row 2 column 1 of the product equal to zero. Consider the product with the following matrix $M$ $$mat{lambda&sigma-sigma&lambda},mat{M_{11}&M_{12}&cdots&M_{1m}M_{21}&M_{22}&cdots&M_{2m}}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=mat{hphantom{-}lambda M_{11}+sigma M_{21}&hphantom{-1}lambda M_{12}+sigma M_{22}&cdots&hphantom{-1}lambda M_{1m}+sigma M_{2m}-sigma M_{11}+lambda M_{21}&-sigma M_{12}+lambda M_{22}&cdots&-sigma M_{1m}+lambda M_{2m}}$$

To find $G_1$, we solve $$begin{matrix}begin{split}-sigma M_{11}+lambda M_{21}&=0text{s.t. }~~~~~~~~~~~~~sigma^2+lambda^2&=1end{split}end{matrix}~~~~~~~implies~~~~~~~begin{matrix}lambda=frac{M_{11}}{sqrt{M_{11}^2+M_{21}^2}}~~~text{and}~~~sigma=frac{M_{21}}{sqrt{M_{11}^2+M_{21}^2}}end{matrix}$$

Now, we can repeat this process to successively make all entries below the diagonal zero, giving us a QR decomposition.

HOMEWORK

Determine the computational complexity for QR decomposition using
- Gram-Schmidt
- Modified Gram-Schmidt
- Householder reflections
- Givens rotations
Compare the complexity of Householder vs Givens for a sparse matrix
Implement QR decomposition using Householder reflections, (input matrix A of full column rank and output Q,R)
Repeat 3 using Givens rotations

$$~$$

'Large' data least squares

$AinRnm$, where $ngg m~~$ (which is a different situation than $mgg n$)

$Householder qr factorization$

Optional reference : 'Incremental QR Decomposition' , by Gentleman.

We can apply QR decomposition to solving the least squares equation $Ax=b$ since
begin{align*}
hat{x}&=(A'A)inv A'b
&=((QR)'(QR))inv(QR)'b
&=(R'cancel{Q'Q}R)inv R'Q'b
&=(R'R)inv R'Q'b
&=Rinvcancel{(R')inv R'}Q'b
&=Rinv Q'b
end{align*}